| No. |
Date |
Topics |
|
Approximation and interpolation |
| 1 |
8/23 |
introduction to class; norms, seminorms, and function spaces |
| 2 |
8/25 |
approximation problems;
existence and uniqueness of best approximation |
| 3 |
8/28 |
Weierstrass Approximation Theorem; Bernstein polynomials |
| 4 |
8/30 |
Bernstein polynomials, Jackson Theorem in C12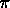 |
| 5 |
9/1 |
Jackson Theorem in
Ck2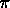 ,
Jackson Theorem inC1 ,
Jackson Theorem inC1
|
| 6 |
9/6 |
Jackson Theorem inCk,
polynomial approximation to analytic functions
|
| 7 |
9/8 |
Characterization and uniqueness of the minimax approximation |
| 8 |
9/11 |
Lagrange interpolation |
| 9 |
9/13 |
theory of Lagrange interpolation, Lesbesgue constants |
| 10 |
9/15 |
Chebyshev polynomials, interpolation at the Chebyshev points,
|
| 11 |
9/18 |
least squares approximation, normal equations, Gram
matrices, Gram-Schmidt |
| 12 |
9/20 |
Legendre polynomials, error estimates in L2
and max norm for least squares approximation |
| 13 |
9/22 |
weighted least squares |
| 14 |
9/25 |
piecewise polynomial spaces in 1D |
| 15 |
9/27 |
error analysis for piecewise Lagrange interpolation and
piecewise Hermite cubic interpolation, cubic spline interpolation |
| 16 |
9/29 |
Bramble-Hilbert lemma |
| 17 |
10/2 |
analysis of cubic spline interpolation, concluded |
| 18 |
10/4 |
piecewise polynomial approximation in 2D |
| 19 |
10/6 |
analysis piecewise polynomial interpolation in 2D |
| 20 |
10/11 |
analysis piecewise polynomial interpolation in 2D |
| 21 |
10/13 |
fast Fourier transform |
|
Numerical quadrature |
| 22 |
10/16 |
quadrature rules |
| 23 |
10/18 |
Peano kernel theorem |
| 24 |
10/20 |
Euler-Maclaurin expansion |
| 25 |
10/23 |
Romberg integration |
| 26 |
10/23 |
Gaussian quadrature |
| 27 |
10/25 |
convergence of Gaussian quadrature, weighted Gaussian quadrature |
| 28 |
10/27 |
adaptive quadrature |
| 29 |
10/30 |
adaptive quadrature |
|
Direct methods of numerical linear algebra |
| 30 |
11/1 |
basic algorithms of numerical linear algebra |
| 31 |
11/3 |
Midterm exam |
| 32 |
11/6 |
elimination and factorization |
| 33 |
11/8 |
Cholesky decomposition, pivoting |
| 34 |
11/10 |
backward error analysis |
| 35 |
11/13 |
condition of linear systems |
|
Numerical solution of nonlinear systems and optimization |
| 36 |
11/15 |
introduction to nonlinear systems |
| 37 |
11/17 |
one-point iterations |
| 38 |
11/20 |
Newton's method |
| 39 |
11/22 |
quasi-Newton methods |
| 40 |
11/27 |
Broyden's method |
| 41 |
11/29 |
convergence of Broyden's method |
| 42 |
12/1 |
unconstrained minimization, steepest descents |
| 43 |
12/4 |
line-search methods |
| 44 |
12/6 |
global convergence of line-search methods |
| 45 |
12/8 |
various complements |
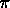
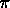 ,
Jackson Theorem inC1
,
Jackson Theorem inC1
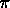
 ,
Jackson Theorem inC1
,
Jackson Theorem inC1